蜣螂优化算法（Dung beetle optimizer，DBO）由Jiankai Xue和Bo Shen于2022年提出，该算法主要受蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为的启发所得。

一、蜣螂优化算法

1.1蜣螂滚球

（1）当蜣螂前行无障碍时，蜣螂在滚粪球过程中会利用太阳进行导航，下图中红色箭头表示滚动方向

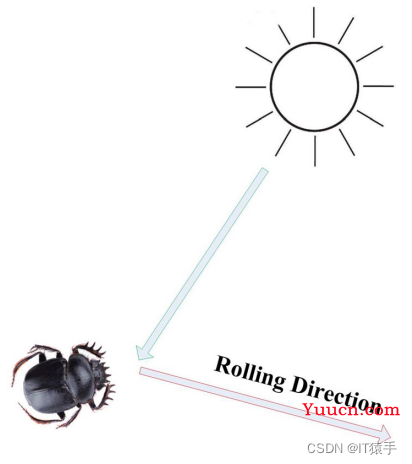
本文假设光源的强度会影响蜣螂的位置，蜣螂在滚粪球过程中位置更新如下：

x
i
(
t
+
1
)
=
x
i
(
t
)
+
α
×
k
×
x
i
(
t
−
1
)
+
b
×
Δ
x
,
Δ
x
=
∣
x
i
(
t
)
−
X
w
∣
\begin{aligned} x_{i}(t+1) &=x_{i}(t)+\alpha \times k \times x_{i}(t-1)+b \times \Delta x, \\ \Delta x &=\left|x_{i}(t)-X^{w}\right| \end{aligned}
xi​(t+1)Δx​=xi​(t)+α×k×xi​(t−1)+b×Δx,=∣xi​(t)−Xw∣​
其中，$t$表示当前迭代次数，
x
i
(
t
)
x_{i}(t)
xi​(t)表示第$i$次蜣螂在第t次迭代中的位置信息，$k\in (0,0.2]$为扰动系数，$b$为 $(0,1)$ 之间的随机数，$\alpha$取 -1 或 1 ，
X
w
X^{w}
Xw表示全局最差位置，$\Delta x$用于模拟光的强度变化。
其中，$\alpha$的取值采用算法1：

（2）当蜣螂遇到障碍物无法前进时，它需要通过跳舞来重新调整自己，以获得新的路线。本文使用切线函数来模仿跳舞行为，以此获得新的滚动方向，滚动方向仅考虑为$[0,\pi ]$之间。

蜣螂一旦成功确定新的方向，它应该继续向后滚动球。蜣螂的位置更新如下：

x
i
(
t
+
1
)
=
x
i
(
t
)
+
tan
⁡
(
θ
)
∣
x
i
(
t
)
−
x
i
(
t
−
1
)
∣
x_{i}(t+1)=x_{i}(t)+\tan (\theta)\left|x_{i}(t)-x_{i}(t-1)\right|
xi​(t+1)=xi​(t)+tan(θ)∣xi​(t)−xi​(t−1)∣
其中，$\theta$为偏转角，其取值为$[0,\pi ]$，采用算法2：

1.2蜣螂繁殖

在自然界中，雌性蜣螂将粪球被滚到适合产卵的安全地方并将其隐藏起来，以此为后代提供一个安全的环境。受此启发，因而提出了一种边界选择策略以此模拟雌性蜣螂产卵的区域：

L
b
∗
=
max
⁡
(
X
∗
×
(
1
−
R
)
,
L
b
)
U
b
∗
=
min
⁡
(
X
∗
×
(
1
+
R
)
,
U
b
)
\begin{array}{l} L b^{*}=\max \left(X^{*} \times(1-R), L b\right) \\ U b^{*}=\min \left(X^{*} \times(1+R), U b\right) \end{array}
Lb∗=max(X∗×(1−R),Lb)Ub∗=min(X∗×(1+R),Ub)​
其中，
X
∗
X^{*}
X∗表示当前最优位置，
L
b
∗
L b^{*}
Lb∗和
U
b
∗
U b^{*}
Ub∗分别表示产卵区的下限和上限，
R
=
1
−
t
/
T
m
a
x
R=1−t/T_{max}
R=1−t/Tmax​，
T
m
a
x
T_{max}
Tmax​表示最大迭代次数，$Lb$和$Ub$分别表示优化问题的下限和上限。
雌性蜣螂一旦确定了产卵区，就会选择在该区域育雏球产卵。每只雌性蜣螂在每次迭代中只产生一个卵，可以看出，产卵区的边界范围是动态变化的，主要由R值决定。因此，育雏球的位置在迭代过程中也是动态的，其定义如下：

B
i
(
t
+
1
)
=
X
∗
+
b
1
×
(
B
i
(
t
)
−
L
b
∗
)
+
b
2
×
(
B
i
(
t
)
−
U
b
∗
)
B_{i}(t+1)=X^{*}+b_{1} \times\left(B_{i}(t)-L b^{*}\right)+b_{2} \times\left(B_{i}(t)-U b^{*}\right)
Bi​(t+1)=X∗+b1​×(Bi​(t)−Lb∗)+b2​×(Bi​(t)−Ub∗)
其中，
B
i
(
t
)
B_{i}(t)
Bi​(t)表示第t次迭代中第 i个育雏球的位置信息，
b
1
b_{1}
b1​和
b
2
b_{2}
b2​均为1×D的随机向量，D表示优化问题的维度。
产卵区的选择如算法3所示：

1.3蜣螂觅食

雌性蜣螂所产的卵会逐渐长大，一些已经成熟的小蜣螂会从地下出来寻找食物，小蜣螂的最佳觅食区建模如下：

L
b
b
=
max
⁡
(
X
b
×
(
1
−
R
)
,
L
b
)
U
b
b
=
min
⁡
(
X
b
×
(
1
+
R
)
,
U
b
)
\begin{array}{l} L b^{b}=\max \left(X^{b} \times(1-R), L b\right) \\ U b^{b}=\min \left(X^{b} \times(1+R), U b\right) \end{array}
Lbb=max(Xb×(1−R),Lb)Ubb=min(Xb×(1+R),Ub)​
其中，
X
b
X^{b}
Xb表示全局最优位置，
L
b
b
L b^{b}
Lbb和
U
b
b
U b^{b}
Ubb分别表示最佳觅食区的下限和上限。

小蜣螂的位置更新如下：

x
i
(
t
+
1
)
=
x
i
(
t
)
+
C
1
×
(
x
i
(
t
)
−
L
b
b
)
+
C
2
×
(
x
i
(
t
)
−
U
b
b
)
x_{i}(t+1)=x_{i}(t)+C_{1} \times\left(x_{i}(t)-L b^{b}\right)+C_{2} \times\left(x_{i}(t)-U b^{b}\right)
xi​(t+1)=xi​(t)+C1​×(xi​(t)−Lbb)+C2​×(xi​(t)−Ubb)
其中，
x
i
(
t
)
x_{i}(t)
xi​(t)表示第t次迭代中第i只小蜣螂在的位置，
C
1
C_{1}
C1​是服从正态分布的随机数，
C
2
C_{2}
C2​为(0,1)的随机向量。

1.4蜣螂偷窃

另一方面，一些蜣螂从其他蜣螂那里偷粪球，盗贼蜣螂的位置更新如下：

x
i
(
t
+
1
)
=
X
b
+
S
×
g
×
(
∣
x
i
(
t
)
−
X
∗
∣
+
∣
x
i
(
t
)
−
X
b
∣
)
x_{i}(t+1)=X^{b}+S \times g \times\left(\left|x_{i}(t)-X^{*}\right|+\left|x_{i}(t)-X^{b}\right|\right)
xi​(t+1)=Xb+S×g×(∣xi​(t)−X∗∣+∣∣​xi​(t)−Xb∣∣​)
其中，
x
i
(
t
)
x_{i}(t)
xi​(t)表示在第t次迭代中第i个盗贼蜣螂的位置，g为服从正态分布的1×D随机向量，S为常数。

二、蜣螂优化算法描述

滚球蜣螂、繁殖蜣螂、觅食蜣螂和偷窃蜣螂的比例分布如下：

DBO算法描述如下：

参考文献：Xue, J., Shen, B. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization. J Supercomput (2022). https://doi.org/10.1007/s11227-022-04959-6