HMER论文系列
1、论文阅读和分析:When Counting Meets HMER Counting-Aware Network for HMER_KPer_Yang的博客-CSDN博客
2、论文阅读和分析:Syntax-Aware Network for Handwritten Mathematical Expression Recognition_KPer_Yang的博客-CSDN博客
3、论文阅读和分析:A Tree-Structured Decoder for Image-to-Markup Generation_KPer_Yang的博客-CSDN博客
4、 论文阅读和分析:Watch, attend and parse An end-to-end neural network based approach to HMER_KPer_Yang的博客-CSDN博客
5、 论文阅读和分析:Multi-Scale Attention with Dense Encoder for Handwritten Mathematical Expression Recognition_KPer_Yang的博客-CSDN博客
6、 论文阅读和分析:Mathematical formula recognition using graph grammar_KPer_Yang的博客-CSDN博客
7、 论文阅读和分析:Hybrid Mathematical Symbol Recognition using Support Vector Machines_KPer_Yang的博客-CSDN博客
8、论文阅读和分析:HMM-BASED HANDWRITTEN SYMBOL RECOGNITION USING ON-LINE AND OFF-LINE FEATURES_KPer_Yang的博客-CSDN博客
主要贡献:
1、提出了一种基于支持向量机的混合识别系统,该系统同时使用在线和离线信息进行分类。
2、并行运行的两个基于支持向量机的多类分类器的概率输出通过加权和进行组合。实验结果表明,赋予在线信息稍高的权重会产生更好的结果。混合系统在单独使用时的整体错误率低于在线和离线识别系统。
复习SVM
下面所说的,在libsvm都有实现
SVMs基于两个观点:VC维度和最小化结构风险。
在VC理论中,最常用的概念为VC维(VC dimension)。VC维度(或Vapnik-Chervonenkis维度)是衡量可以通过统计分类算法学习的函数空间的容量(复杂度,表现力,丰富度或灵活性)的度量。它被定义为算法可以破碎(shatter)的最大点集的基数,在这里破碎(shatter)意为若对于一个假设空间H,如果存在m个数据样本能够被假设空间H中的函数按所有可能的2^h种形式分开,则称假设空间H能够把m个数据样本破碎(shatter)。在二维平面上的简单理解就是可以使得线性划分数据集所有点类别的最小直线数目。
SVMs遇到线性不可分的情况下,理论上在一个更高的维度空间可以线性可分,相当于给一个非线性决策平面在原来的特征空间。可以表示成:
f
(
x
)
=
∑
i
α
i
y
i
K
(
x
,
x
i
)
+
b
f(x)=\sum_i\alpha_iy_i K(x,x_i)+b
f(x)=i∑αiyiK(x,xi)+b
y
i
y_i
yi:label;
x
i
x_i
xi:训练样本;
x
x
x:待分类样本;
K
(
x
,
x
i
)
=
ϕ
(
x
)
ϕ
(
x
i
)
K(x,x_i)=\phi(x) \phi(x_i)
K(x,xi)=ϕ(x)ϕ(xi):核函数:
K
(
a
,
b
)
=
exp
(
−
γ
∣
∣
a
−
b
∣
∣
2
)
,
γ
>
(radial basis fns)
K
(
a
,
b
)
=
(
γ
(
a
⋅
b
)
+
r
)
d
,
γ
>
(polynomial)
K
(
a
,
b
)
=
tanh
(
γ
(
a
⋅
b
)
+
r
)
(sigmoid)
\begin{array}{l} K(a,b)=\exp(-\gamma||a-b||^2),\gamma>0\text{(radial basis fns)}\\ K(a,b)=(\gamma(a\cdot b)+r)^d,\gamma>0\textrm{(polynomial)}\\ K(a,b)=\tanh(\gamma(a\cdot b)+r)\textrm{(sigmoid)} \end{array}
K(a,b)=exp(−γ∣∣a−b∣∣2),γ>0(radial basis fns)K(a,b)=(γ(a⋅b)+r)d,γ>0(polynomial)K(a,b)=tanh(γ(a⋅b)+r)(sigmoid)
一般而言,SVMs用于二分类任务,多分类任务用DAG and one-against-one作为多分类的实现。
同时,要让SVMs输出后验概率,需要使用sigmoid函数:
p
(
y
=
1
∣
f
(
x
)
)
=
1
1
+
exp
(
A
f
(
x
)
+
B
)
p(y=1|f(x))=\dfrac{1}{1+\exp(Af(x)+B)}
p(y=1∣f(x))=1+exp(Af(x)+B)1
f
(
x
)
f(x)
f(x):SVM的输出;A和B:可以从负的log-likelihood 函数在训练数据得到;
架构
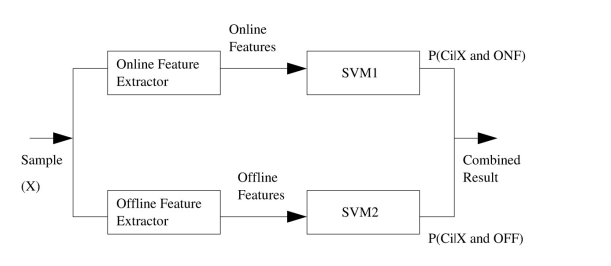
使用在线特征和离线特征,通过两个不同的SVM分类器,得到每个类别的概率,联合求出总的概率,得到结果。
联合:
P
(
C
i
∣
X
)
=
α
P
(
C
i
∣
X
,
O
N
F
)
+
β
(
C
i
∣
X
,
O
F
F
)
P(C_i|X)=αP(C_i|X,ONF)+β(C_i|X,OFF)
P(Ci∣X)=αP(Ci∣X,ONF)+β(Ci∣X,OFF)
α
+
β
=
1
\alpha + \beta = 1
α+β=1
在线特征向量
预处理:
1、smoothing:使用中心平滑去平滑墨水的笔迹;
x
i
=
0.25
x
i
−
1
+
0.5
x
i
+
0.25
x
i
+
1
y
i
=
0.25
y
i
−
1
+
0.5
y
i
+
0.25
y
i
+
1
\begin{array}{rcl}x_i&=&0.25x_{i-1}+0.5x_i+0.25x_{i+1}\\ y_i&=&0.25y_{i−1}+0.5y_i+0.25y_{i+1}\end{array}
xiyi==0.25xi−1+0.5xi+0.25xi+10.25yi−1+0.5yi+0.25yi+1
2、Filling intermediate points:在连续的点之间填充内部点,这样对齐空间,没有对齐时间,因为发现空间对齐比时间对齐更有用。因此,在重新采样时,我们将笔画上的点放置在相等的距离上。
3、resample重采样:每个笔画选择每
N
/
1
1
t
h
N/11^{th}
N/11th的点,N是总的点数;
4、size normalization尺度归一化:每个stroke使用
1
/
m
a
x
(
h
,
w
)
1/max(h,w)
1/max(h,w)进行归一化;
提取特征:
发现坐标和角度信息是最有区分度的特征,增加图形特征例如相关长度,错误率降低很小但是特征向量更多;
计算重心:
∑
i
(
x
i
/
N
)
,
∑
i
(
y
i
/
N
)
,
\sum_i(x_i/N),\sum_i(y_i/N),
i∑(xi/N),i∑(yi/N),
转过的角度:

因此得到的特征包括:
| 特征: |
|---|
| stroke笔画的每个点的坐标 |
| line segments的sines和cosines值 |
| line segments和符号重心的sines和cosines值 |
离线特征向量
1、离线特征是将stroke转换成图片,存储样本文件在InkML格式,这些文件加载使用black ink在white背景上,使用Microsofts Tablet PC SDK.
2、转换到bitmap后,进行尺度缩放:
15
/
m
a
x
(
w
,
h
)
15/max(w,h)
15/max(w,h)。
3、使用high-quality bilinear interpolation filter,填补边缘得到bitmap 15*15大小。

提取的特征:
| 特征: |
|---|
|
( I 1 , I 2 , . . . , I N ) (I_1,I_2,…,I_N) (I1,I2,…,IN):灰度强度像素点的值 N = w ∗ h N=w*h N=w∗h。 |
参考:
《Hybrid Mathematical Symbol Recognition using Support Vector Machines》
VC维度 | 机器之心 (jiqizhixin.com)

近期评论